Internet :
mathkang.com
bibmath.net
proftnj.com
math93.com
mathcurve.com
serge.mehl.free
sous-mama.org
onversity.net
volcan.dufouraubin.com
fr.wikipedia.org
eauplaisir.com
auvergne.iufm.fr
worldlingo.com
Livres :
Mathématiques et mathématiciens :écrit par Pierre Dedron et Jean Itard; paru aux éditions magnard paris; (page 84-85);
Archimède a réalisé des travaux en mathématiques si importants qu'ils sont présents dans la vie de tous les jours : Le nombre PI est utilisé pour calculer des perimètres, des aires et des volumes,donc une importance dans de nombreux domaines de construction. La Spirale d'Archimède, utilisée dans des mecanismes utilisés dans la vie de tout les jours, la poussée d'Archimède permet de comprendre des phénomènes naturels, de plus on s'en sert pour construire divers mécanismes et pour les moyens de transports. C'était un savant de l'Antiquité, on utilise encore ses apports importants 2200 ans plus tard.
d) Utilisation
La Poussée d’Archimède est présente dans le déroulement de l'éruption d'un volcan les sables mouvants, de plus, elle est utilisée dans la construction navale de bateaux et de sous-marins, permet d’expliquer le fonctionnement des systèmes de déplacement d’eau comme dans les piscines, elle est utilisée dans le fonctionnement de montgolfières ou dirigeables.
Voici un exemple :
LE SOUS-MARIN
Nous avons vu que tout corps plongé dans un liquide reçoit de la part de ce liquide une poussée verticale de bas en haut, égale au poids du volume de liquide déplacé.
Le sous-marin dans l’eau de mer est soumis à deux forces :
-son poids, appliqué au centre de gravité (G), force verticale dirigée de haut en bas. Elle tend à faire descendre le sous-marin. -la poussée d’Archimède appliquée au centre du volume immergé (C), force verticale dirigée vers le haut. Elle tend à faire remonter le sous-marin. L'équilibre est obtenu quand le poids de l'eau déplacé, c'est à dire la poussée, correspond au poids du sous-marin
Si par exemple le sous-marin est en surface, les ballasts sont vides. Le sous-marin flotte, il est donc en équilibre. Le poids du volume d’eau déplacé est bien égal au poids du sous-marin comme dans le dessin montré ci-dessous.
Si maintenant on ouvre le système d’ouverture des ballasts appelé purge, ils se rempliront d’eau, le sous-marin va donc s’alourdir et s’enfoncer. Le poids du volume d’eau supplémentaire déplacé sera donc égal au poids de l’eau contenu dans les ballasts. Un nouvel équilibre est donc trouver. A chaque volume d’eau rajouté en plus dans les ballasts, le sous-marin s’enfonce un peu plus, un nouvel équilibre est donc obtenu.
En immersion totale maintenant, les ballasts sont totalement remplis d’eau de mer. Si l’on vide ces ballasts en remplaçant l'eau de mer par de l'air contenu dans des bouteilles d'air situées à l'intérieur du sous-marin. Le poids du sous-marin diminue du poids du volume d'eau évacué des ballasts : la poussée, est supérieure au poids du bâtiment. Il devient "léger" et remonte. La valeur de la poussée diminuant avec la hauteur de l’immersion, on obtient donc un nouvel équilibre poids/poussée.
c) Étude de la force :
La poussé d'Archimède est la force qui résulte d'un ensemble d'actions mécaniques de pression ; elle est répartie sur la surface d'un objet partiellement ou totalement immergé.
On la note : Fa
Les caractéristiques de cette force sont :
_Point d'application : La poussée d'Archimède s'applique au niveau du centre de gravité (G) du système immergé.
_Direction : verticale
_Sens : vers le haut
_Norme : L'intensité de la poussée d'Archimède est égale à la valeur du poids du fluide déplacé. Pour la calculer, on note alors la formule suivante : FA=gxVix ρfluide
On peut également calculer l'intensité de la force en utilisant cette formule :
FA = G - Gapp Gapp = G - FA
FA
poussée (ou force) d'Archimède en [N]
ρfluidemasse volumique du fluide en [kg/m3]
b) Propriétés :
Voici une animation interactive où l'on peut observer différentes propriétés :
a) énoncé
Commençons d'abord par énoncer le principe :
"Tout corp plongé dans un fluide subit de la part du fluide une force verticale dirigée de bas en haut. Cette force est égale au poids du volume du fluide déplacé"
La
force dont il est question ici se nomme aussi la poussée d'Archimède.
Remarque : on parle de fluide et non seulement de liquide. En effet le principe d'Archimède s'applique non seulement pour les liquides comme l'eau, mais aussi pour les gaz comme l'air.
Observons un exemple sur l'animation suivante :
(si c'est écrit "abonnez vous" il faut réactualiser la page)
c) Utilisation :
*Définition de la quadrature :
En calcul intégral, c’est une opération consistant à déterminer l'aire comprise à l'intérieur d'une courbe fermée.
Elle a été introduite par Archimède pour réussir la quadrature du cercle*, c'est-à-dire la construction d'un segment dont la longueur est égale à la circonférence du cercle.
Prenons en effet le point sur la courbe de coordonnée polaire t=3pi/2 (le point A du dessin précédent).
Traçons la tangente à la spirale en ce point, et notons H le point d'intersection avec l'axe des abscisses.
Alors Archimède démontre que la longueur AH vaut exactement la circonférence du cercle OA.
Cependant, cela ne fait que déplacer le problème : comment construire la tangente à une courbe?
Il faudra attendre au moins le XVIIè siècle, et Newton et Leibniz, pour que l'on sache bien aborder cette question!
Aujourd'hui, la spirale d'Archimède a énormément d'applications réelles :
_Les compresseurs de rouleaux (également appelés compresseurs en spirale) sont faits à partir de deux palettes en forme de spirales d'Archimède de la même taille, ils sont employé pour comprimer des liquides et des gaz.
_Dans une montre à ressorts compensateurs les ressorts sont en forme de spirale d'Archimède.
_Les cannelures sur les disques phonographes forment une spirale d'Archimède, pour maximiser la quantité de musique qui pourrait être adaptée sur le disque( ceci a été changé plus tard pour obtenir une meilleure qualité de son).
_Demander un patient pour dessiner une spirale d'Archimède est une manière de mesurer le tremblement humain; cette information est utile pour diagnostiquer les maladies neurologiques.
_Des spirales d'Archimède sont également employées dans les DPL (Digital Light Processing) : traitement numérique de la lumière (TPL), des composants utilisés dans les rétroprojecteurs; ce sont systèmes de projection pour réduire au minimum le « effet d'arc-en-ciel », qui permettent d'obtenir à la vision des couleurs multiples en même temps quand en réalité rouge, verts, et bleu sont extrêmement rapides faits un cycle.
_ L'intersection de la spirale avec
une droite passant par le centre décrit un mouvement uniforme (ceci
sert à transformer un mouvement circulaire en mouvement rectiligne,
par exemple pour le remplissage régulier d'une bobine de fil ou
les anciennes machines à coudre.
b)Définition de la courbe
Cette
spirale
est l'ensemble des points M se déplaçant d'un mouvement uniforme sur une droite
en rotation uniforme autour d'un point.
Trajectoire d’un point se déplaçant uniformément sur une droite d’un
plan, la droite tournant autour d’un de ses points d’un mouvement
uniforme.
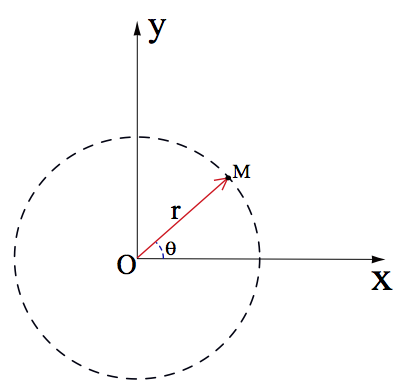
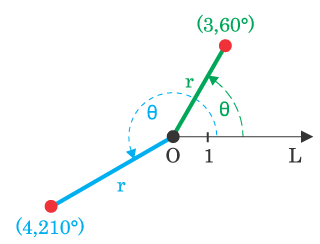
Définition de l’équation polaire : Une courbe est dite définie en coordonnées polaires si tout point M(r,θ) de cette courbe vérifie une équation (ou plusieurs simultanées si nécessaire : définition par morceaux) de la forme r = f(θ) où f est une fonction de θ (variant éventuellement dans un ensemble J précisé). Le problème est parfois (souvent) de rechercher l'ensemble J minimal permettant l'obtention de la courbe en entier.
A cause de la forme circulaire des coordonnées polaires, beaucoup de courbes peuvent être décrites comme une équation polaire simple, alors que leur équation cartésienne serait beaucoup plus compliquée.
La spirale d'Archimède a pour équation polaire : ρ= a θ qui s'écrit aussi r= a x t
On peut exprimer l'équation polaire : r(θ)= a+b θ
ρ ou r= distance du point par rapport au pôle O sur le rayon
a= paramètre non nul
θ ou t=angle polaire de M (exprimé en radians)
Changer le paramètre a tourne la spirale, alors que b donne la distance entre les spires, qui pour une spirale donnée est
constante. Une spirale d'Archimède possède deux bras, l'un pour θ > 0 et l'autre pour θ < 0.
Les deux bras sont connectés au pôle.
Chaque bras est le symétrique de
l'autre par rapport à l'axe vertical (90°/270°).
Cette courbe est l'une des premières courbe à être décrite par des termes mathématiques et à être un exemple de courbe simplement exprimée dans le système des coordonnées polaires.
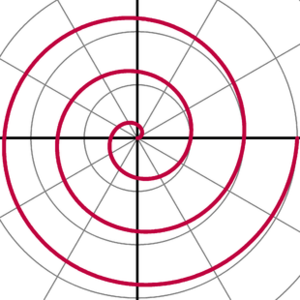
Un bras d'une spirale d'Archimède d'équation r(θ) = θ pour 0 < θ< 6π
La prise de l'image de miroir de ce bras à travers l'axe des ordonnées rapportera l'autre bras où on aura les valeurs angulaires de la courbes θ < 0 .
Si on trace la spirale
pour tout t réel, on obtient une symétrie par rapport
à Oy
a) Coordonnées polaires
En coordonnées polaires, la position du point M est définie par la distance r et l'angle θ.
Un cercle découpé en angles mesurés en degré
En mathématiques, il existe 2 systèmes de coordonnées en 2 dimension :
_le systèmes des coordonnées cartésiennes
_le système des coordonnées polaires
Dans le système de coordonnées polaires, chaque point du plan est déterminé par un angle et une distance.
Ce système est utile dans le cas ou la relation entre 2 points est plus facile avec des angles et des distances.
Par exemple dans le cas du pendule.
Si on utiliserait des coordonnées cartésiennes, on devrait utilisait des formules trigonométriques pour exprimer une telle relation.
Vu qu'il s'agit d'un système en 2 dimension, chaque point déterminé par des coordonnées polaires :
_la coordonnée radiale : notée (r ou ρ) correspond au rayon (voir schéma 1), c'est à dire la distance du point à un point central, O appelée pôle qui correspond à l'origine 0 des coordonnées cartésiennes.
_la coordonnée angulaire : appelée angle polaire ou azimut, elle est notée (t ou θ), elle exprime la mesure, dans le sens trigonométrique (sens positif), de l'angle entre le point et la demi-droite d'angle 0°, appelée axe polaire qui correspond à l'axe des abscisses des coordonnées cartésiennes.
Les points (3;60°) et (4;210°) en coordonnées polaires
Par exemple, le point de coordonnées polaires (3;60 °) sera placé à trois unités de distance du pôle sur la demi-droite d’angle 60 °. Le point (-3 ;-120 °) sera au même endroit car une distance négative sera considérée comme une mesure positive sur la demi-droite opposée par rapport au pôle (tournée de 180 ° par rapport à la demi-droite d’origine). Bref, comme si l'on regardait le plan en se trouvant de l'autre côté.
Il existe une caractéristique unique au système de coordonnées polaires : il existe une infinité de coordonnées polaires désignant un même point. En effet, on peut rajouter des mesures d'un tour complet sans modifier l'emplacement du point, si l'on ajoute ou soustrait 360° à la coordonnée angulaire alors le point a la même position.Par exemple, le point (3;420 °) est confondu avec le point (3;60 °)
b) Utilisation
Le nombre Pi est utilisé dans nombreuses formules, dans des domaines tels que la physique, l'ingénierie et les mathématiques, π est une des constantes les plus importantes des mathématiques.
Pi apparaît dans les formules :
